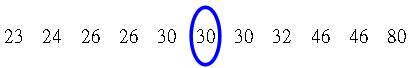量性資料分析以統計應用為主,分為描述統計 (descriptive statistics) 和推論統計 (inferential statistics) 兩大類。前者把基本變項的分佈和數值呈現,進行摘要分析,以較簡單的方法(如交互表列)初探變項間的關係。後者則以較繁複的統計技巧驗證變項之間的機率關係,並非中學程度的同學所能應付。正因如此,本課將集中探討描述統計技巧,並示範一些簡單而有效的Excel工具,以探索數據和檢視變項間可能存在的相互關係。
在「面對面」式導修課(課題二「數據及資料整理」)中我們的導師會帶領學員以此案例做一次excel練習,包括單變項、雙變項統計及交互表列的使用。
2.2.1 單變項描述統計(univariate descriptive statistics)
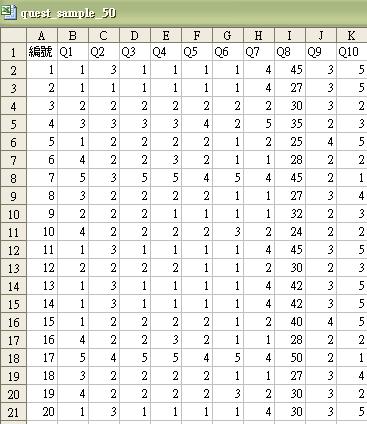
假設我們蒐集了50份有關父親自我形象的問卷調查,而資料已按先前建議的模式記錄於以下檔案。
·
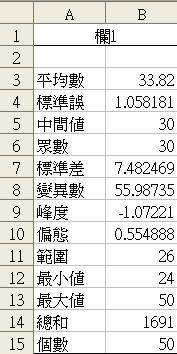
模擬數據:父親的自我形象(問卷數目 = 50)
|
|
|
(a) 分佈 (distribution)
描述分析最基本的工作便是審視數據的分佈。對這份模擬問卷調查,我們想探究的是父親自我形象。由於我們把自我形象操作化為三個面向,而每個面向之下再有類分,我們首要的工夫便是把每個變項 (Q1至Q10) 的資料做一個簡單的分佈描述:
|
|
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
儘管我們的探究問題是Y,這階段的單變項描述統計必須包括 Y 以外的資料,即Q8至Q10的數據。原因是我們需要知道樣本屬性的實質分佈,包括年齡、教育程度以及收入階層。X 變項的分佈能幫助我們審視數據可能出現的誤差。例如,Q1至Q7 的數據可能顯示父親的自我形象頗高,然而,當我們細看 Q10 的分佈資料後,卻發覺大部份受訪者都來自高收入階層。假設兩個同學同時進行這項探究,來自A探究的Q10分佈相對均勻,B探究之樣本則大多數來自高收入階層。如是者,A探究所能提供的資料將較多元豐富,容許我們較有力地比較階層間的差異,並更有信心地就父親自我形象這課題下相對較具普遍性的結論。
(b) 項目個數和百份比分析
拿Q2為例子,問題涉及父親們對自己提供情感關懷和支持的能力之自我評價。我們可借助Excel軟件,快速了解各答項的基本分佈。步驟如下:
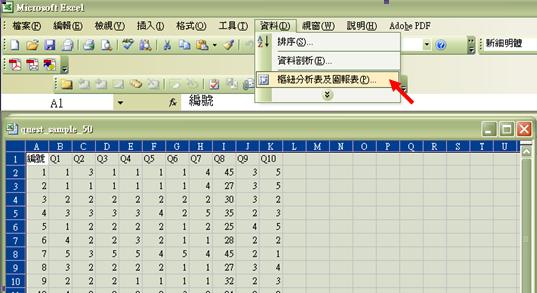
- 先把工作頁打開,然後按紅色箭咀顯示之左上方格,以全選表列資料
- 後拉下功能表之資料清單,選取「樞紐分析表及圖報表」(Pivot table),然後按「下一步 」
|
|
|
|
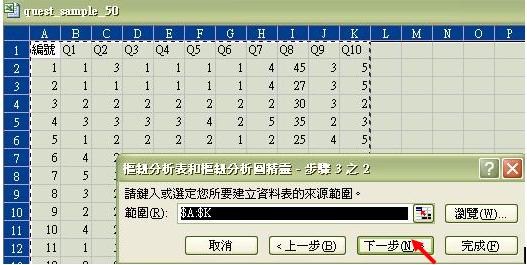
- 圖中顯示的正是你所選取的分析範圍,亦即A欄至 K欄之所有資料。範圍正確的話,可按「下一步」以選取分析欄列
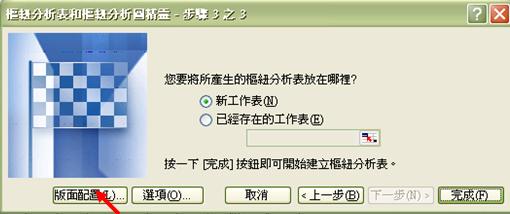
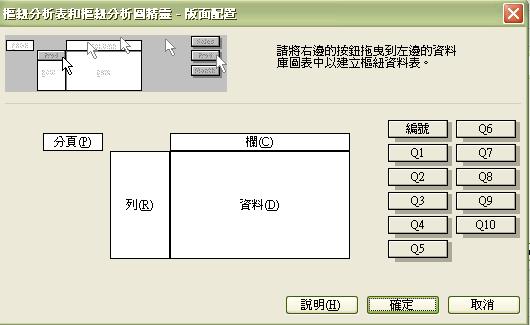
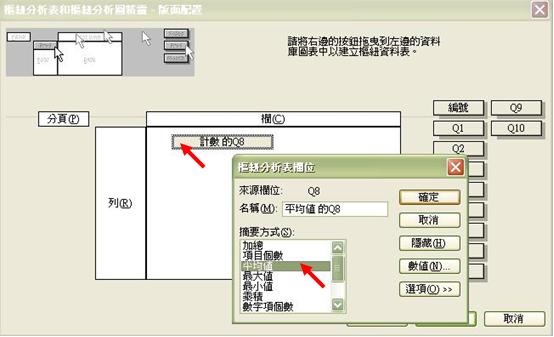
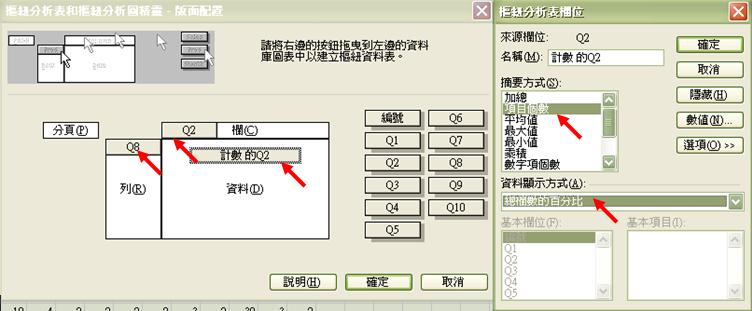
- 這是最關鍵的部份,我們須指示軟件設置那些欄和列做分析。我們可先按下「版面配置」
- 版面配置的左邊是模擬的欄、列排置,右方則設有所選取數據範圍內的所有問題編號。我們只需根據指示,把右邊相關的按鈕拖曳至左邊便可。
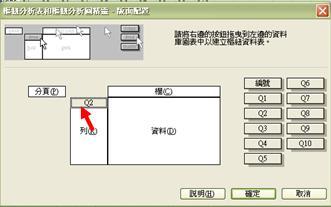
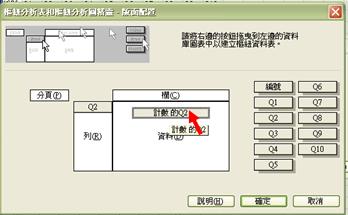
- 假設我們想了解 Q2 的答項分佈,我們只需參照以下左圖,先把Q2拖曳至列的範圍,然後再按右圖顯示,再一次把 Q2 拖曳,但這次卻放在欄目處:
|
|
|
|
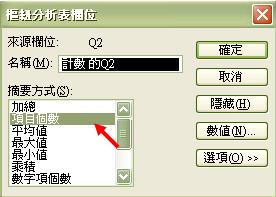
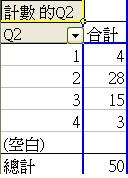
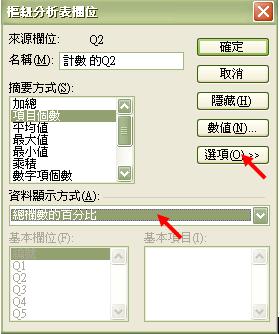
軟件收到這些指令,便知道我們想探究Q2的內容。然而,我們還欠一個指令步驟,告訴軟件所顯示的是什麼有關Q2的數據。我們可把滑鼠放置「計數的Q2」之上,然後點擊兩下,便會彈出樞紐分析表欄位的摘要方式選項。需留意是,Q2的答案屬於等級 / 順序變項 (ordinal measures),各答項之間的間距只顯示累退的邏輯,不能以加減方法來計算實質的差別。在這情況下,計算平均值等資料完全沒有意思,我們需要知道的只是簡單的項目個數,即每個答項的總數目。
|
|
|
|
- 為方便審視資料,我們可進一步指示軟件把項目個數轉成百份比。我們可先按下選項,然後在「資料顯示方式」的下拉表單中選擇「總欄數的百分比」
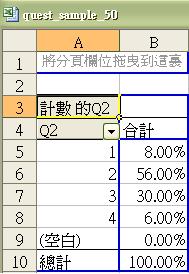
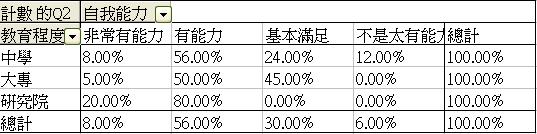
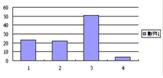
- 按確定後,便能得出以下表列。圖中顯示沒有一個受訪者自我評定為(5- 毫無能力),但選擇 (1- 非常有能力)、(2 - 有能力)、(3 - 基本滿足)和 (4 - 不是太有能力)則分別有8%、56%、30% 和 6%。
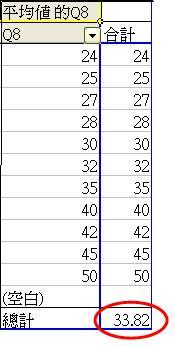
(c) 項目平均值和最大、最小值
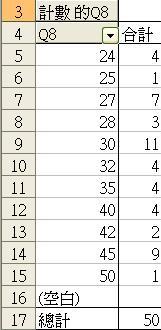
- Q2 變項的測量尺度較適合以項目個數和百份比計算,享有連續變值的變項(如收入、年齡、溫度)則可考慮附加其他方法計算分佈。假設我們重複先前的步驟,並計算出下左圖的項目個數表列。我們希望進一步了解樣本的平均值和最大、最小值。如是者,我們可把滑鼠移放在右圖「計數的Q8」之上,點擊兩下,便會彈出樞紐分析表欄位之選項。我們可選擇「平均值」,然後按確定,便會得出新的表列。
|
|
|
|
|
|
- 我們亦可重新建立一個表列,把Q8拖曳至欄內三次,分別設定計數的Q8為「平均值」、「最大值」和「最小值」。由於我們計算的數目,與列項並不相關,故我們亦不用把Q8拖曳至列,只需根據以下示範操作便行。
(d) 圖表顯示
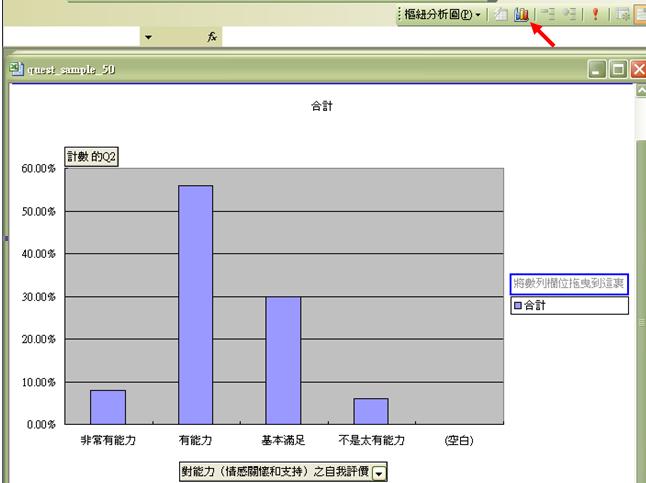
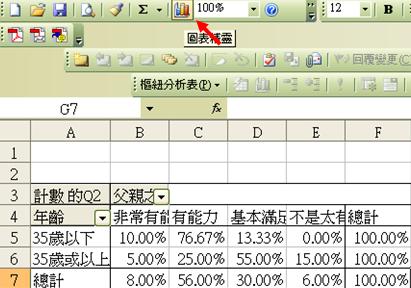
- 以上資料更可以圖表形式顯示,同學可先填寫Q2以及1至4等數字所代表的是什麼,然後拖曳所需繪圖的資料,如B5至B8之數據,右按滑鼠,選取「樞紐分析圖」,便會顯示相關圖表
|
|
|
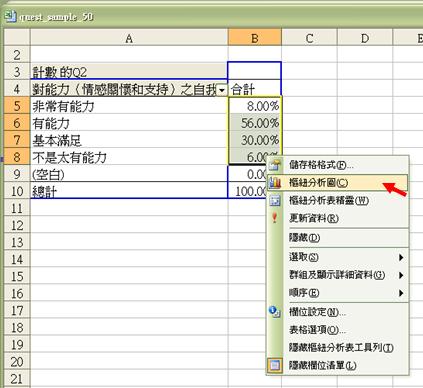 |
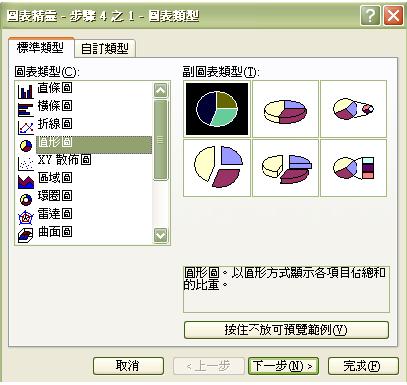
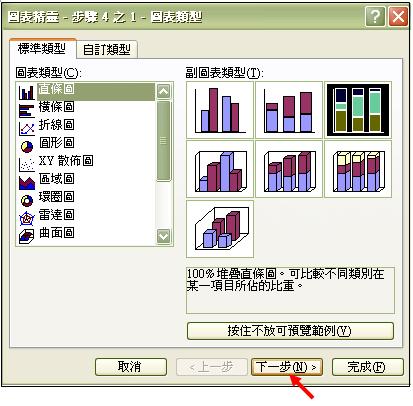
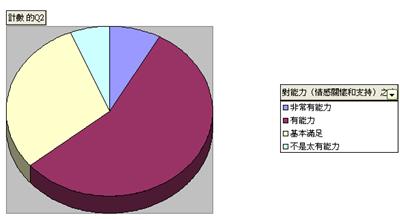
- 同學如不喜歡自動出現的樞紐分析圖,可按上圖右上角的「圖表精靈」,另選圖表類型
|
|
|  |
2.2.2 雙變項分佈 (bivariate distribution) 和 交互表列 (cross-tabulation)
(a) 基本的雙變項分析
Excel 的樞紐分析工具還可提供十分有用的雙變項分佈分析。雖然同學未必會使用到雙變項分析去作母群的推論,但仍可利用此方法探討變項間之關係的強弱,根據早前設計,我們可探索的雙變項關係包括:
|
Xs |
|
Ys |
· 父親之自我形象 (y1-7) 會否因年齡 (x1)而異?
· 父親之自我形象 (y1-7) 會否因教育程度 (x2) 而異?
· 父親之自我形象 (y1-7) 會否因收入 (x3) 而異?
讓我們示範如何探索年齡 (Q8) 和能力(Q2) 之相互關係,步驟如下:
- 先把Q2拖曳至欄目
- 把Q8拖曳至列,指令軟件顯示不同年齡之Q2選項
- 我們需留意如何選擇資料顯示方式。在這情況下,我們依然是選擇計算項目個數,並指令軟件顯示總目的百份比。然而,我們應該選擇「總欄數」抑或「總列數」的百分比呢?軟件只會盲從跟隨我們的指示,而每個指令都會產生一組數字,但那個計算方法才有意思,則需小心思量才是。如我們選擇顯示「總欄數的百分比」,則計算每個年齡類別以內,選取不同Q2答項的百分比。如我們選擇顯示「總列數的百分比」,便是指令軟件計算每個Q2答項以內之年齡百分比。
由於此組模擬數據沒有控制各年齡層的受訪數目,計算「總列數的百分比」可能沒有多大意思,或只會反映樣本中不平均的年齡分佈。在此情況下,「總欄數的百分比」更
能提供有關年齡層之間的分別,幫助我們比較這變項與父親自我形象的關係。當然,我們還須考慮年齡之單變項分佈。如年齡之間的樣本分佈甚不平均,或個案數目
太少,所得來的數據亦未必太有意思。總而言之,探究員還是需要清晰概念邏輯,小心衡量和評估資料該如何詮釋,才能確定哪些是可用的資料,哪些需要進一步補
充。
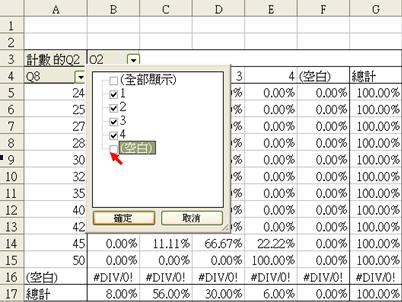
上圖為初步分析。要刪除空白欄列,可拉下Q2 或 Q8之表單,剔除「空白」一欄,便會出現右方的表列。
|
|
|
|
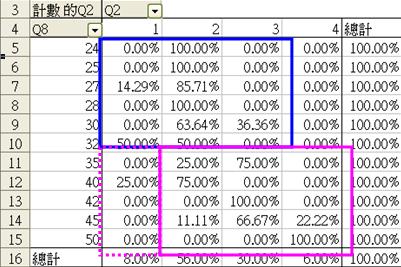
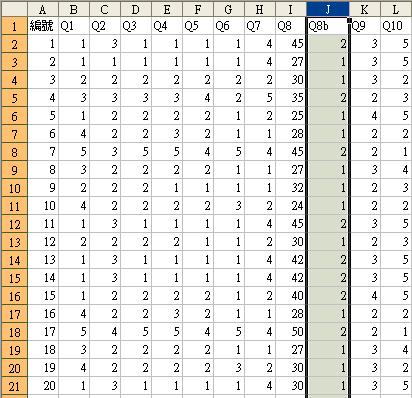
初步觀察,沒有一個受訪者認為自己(5 - 毫無能力),而年齡在35歲或以上的受訪者較多選擇(3 - 基本滿足)或(4 - 不是太有能力)。視乎探究員的判斷和數據的型態,我們可選擇把資料重組以方便審視。例如,我們可以35歲為界線,把來自Q8的資料重組為兩個年齡層,分別為35以下和35或以上。我們須重新打開工作頁,並新增一個欄目(如下圖的Q8b),根據Q8之數據重新鍵入Q8b下之編碼 (1 = 35歲以下,2 = 35歲或以上)。為免錯誤刪改本來的檔案,我們建議同學把所有進一步修正的工作表重新命名,然後另存檔案。
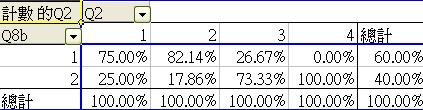
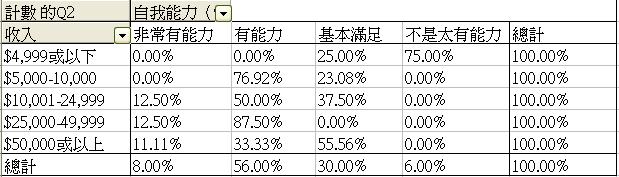
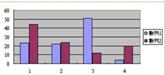
- 我們可使用重整的數據,重複先前步驟,建立新的交互表列。如下圖示,重新編碼的資料能更簡單明確顯示年齡和自我能力評估的關係
- 我們亦可以圖表顯示有關資料。由於我們是比較兩個年齡層之自我形象評價,所使用的數據必須以百分比顯示,並以個別年齡層的總樣本數目為基數計算。以上表列滿足此項要求,適用之圖表有100%堆疊直條圖。我們可按功能表之「圖表精靈」選項,另選圖表類型
|
|
|
|
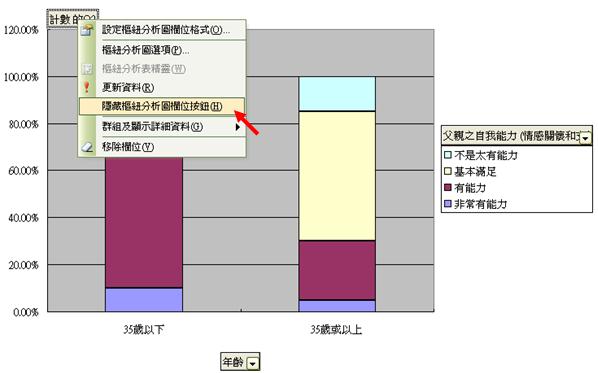
- 如想隱藏樞紐分析圖欄位按鈕的圖示,則只需把滑鼠移至「計數」位置,然後右按,點擊下圖箭咀之選項便是。
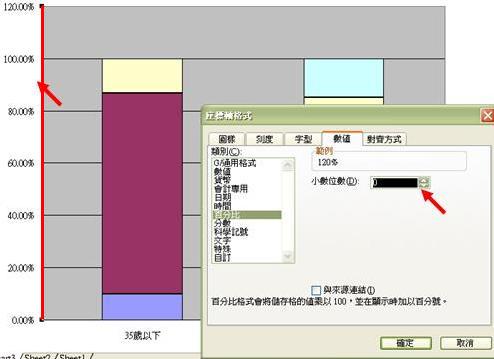
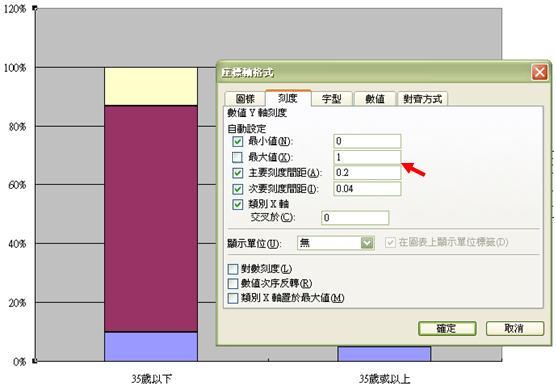
如想進一步修正左欄之百分比數目,把小數位數刪去,並將最大數目定為100,則可把滑鼠移至圖表的Y軸(即紅線圖示),點擊兩下,然後在「數值」選項中把小數位數改至0。確定以後,重復程序並在「刻度」選項中把最大值改為 1,再按確定。
|
|
|
|
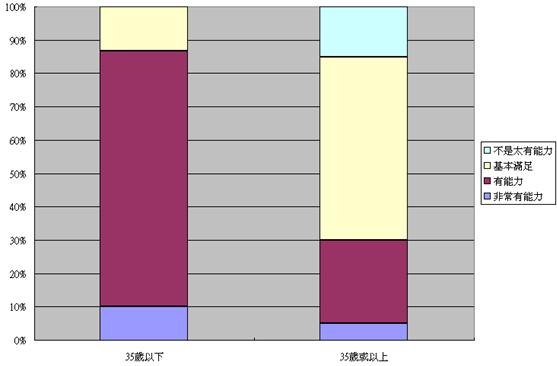
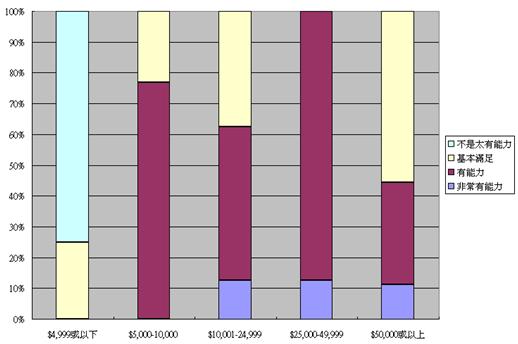
完成以上的程序後,便會出現以下圖表。同學加上適當的標題,便可用於探究報告中:
|
練習 - 嘗試使用模擬數據,建立一個探索Q5和Q10的雙變項交互表列。(示範答案) - 對上述示範有充份掌握的老師,更可考慮把Q10的資料重新編碼,進一步把表列簡化。
|
(b) 詮釋變項之間的關係
圖
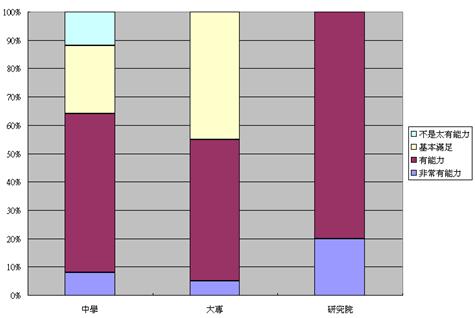
表能更清晰和直接的顯示兩個年齡層的分別。根據以上之模擬數據,父親在情感上的自我評價普遍合格,只有少數覺得自己不是太有能力。然而,年紀較輕的父親之
自我評價似乎較高。圖表顯示了兩個變項之相互關係,但並不代表這便是一個因果關係。我們須追問兩個年齡層之差異因何而來,會否跟樣本中的收入和教育程度分
佈有關呢?要查探這些問題,我們可就不同的變項配搭繪製交互表列和相關圖表。例子如下:
|
年齡組別之單變項分佈 |
|
|
|
|
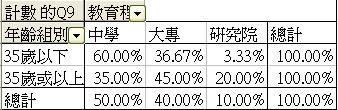
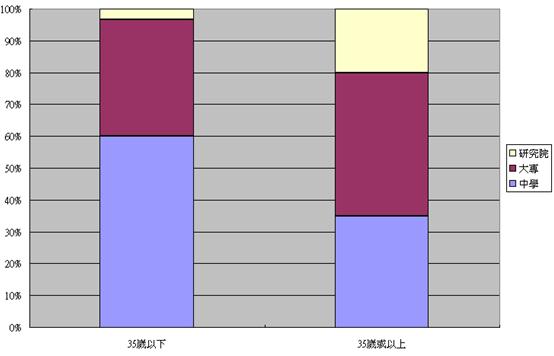
以下之雙變項表列顯示兩個年齡組別的屬性其實有所不同,35歲或以上的受訪者普遍有較高的教育程度和收入。我們必須考慮各個X (年齡、教育程度、收入)對自我形象 (Y) 可能產生的效應,在報告中仔細分別解述,才能有效地舉證以及立論。
|
年齡組別和教育程度之相互關係 |
|
|
|
|
|
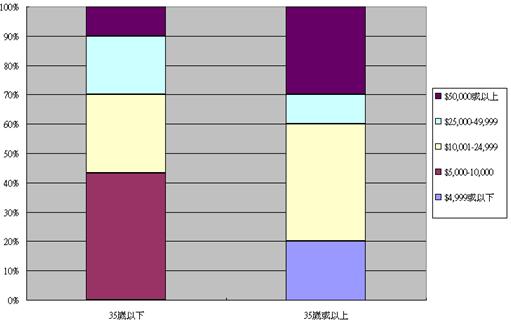
年齡組別和收入之相互關係 |
|
|
|
|
為探討其他兩個 X 變項 (收入、教育程度)和 Y 變項 (如Q2)的關係,我們可建立以下表列:
|
教育程度和自我能力 (情感) 評價之相互關係 |
|
|
|
|
|
收入和自我能力(情感)評價之相互關係 |
|
|
|
|
可 想而知,我們將在這過程中建立不少圖表。部份資料可能支持我們原來的推論,亦可帶來意想不到的發現。我們需在原有的概念框架下,有耐性並開放地審視各項資 料,才能理解數據所反映的真相。先前花了很多篇幅強調概念操作化和抽樣的科學程序,正是為了確保這階段的資料充分,而且可信有效。假若先前的程序太隨意或 是欠缺系統— 只搜集有關自我形象的問題,忽略了查問受訪者的年齡、教育程度和收入;或在量度自我形象之時,只籠統測量了一個面向的現象,則這階段的資料會很單薄,所能進行的分析亦會有限,縱有軟件幫助也無補於事。
老師可嘗試利用這個模擬數據,繪製不同圖表並就自我形象的不同面向進行分析。我們將在第四課續用這些資料,討論如何把這些數據過濾整理,以撰寫探究報告。
2.2.3 其他基本工具和圖表
總括而言,較適用於中學專題探究的描述統計有以下幾類:
(a) 分佈 (distribution)
分佈統計的意思是按資料分類來計算項目分佈,先前的討論亦集中示範分佈統計之單變項和雙變項分析。相關的統計項目包括:
· 頻數 (frequency):即簡單的個數分析
· 百分比 (percentage):以百份數為基數,比較不同變值之比例;另見百分比之補充示範
· 比例 (proportion) :不同變值之相對比重,功能和百份比相似,只是沒有以百份數作為基數計算
· 比率 (ratio):即兩個數值之比值,如男生 (n=40) 相對女生 (n=60) 的比率 = 4:6
(b) 集中趨勢 (central tendency)
除分佈配外,我們也想了解每個變項(如年齡)變值之最佳代表值。一般來說,我們可計算變值之中心位置,而計算方法有三種:
- 平均數 (mean) :數值總和除以項目個數
- 中位數 (median) :即把數值由少至大排列,最中間位置的數值
- 眾數 (mode) :出現最多的數值
|
假設樣本只有十一個個案,年齡分別為: |
三個數值的計算方法不同,眾數考慮個數的數量,而中位數則以距離為依歸,減少了一些極端個案(如例子中最後一個80歲的個案)可能帶來的影響。
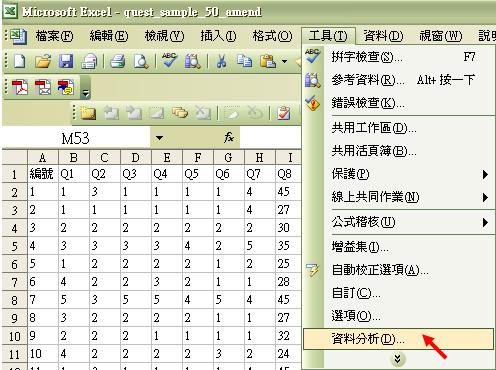
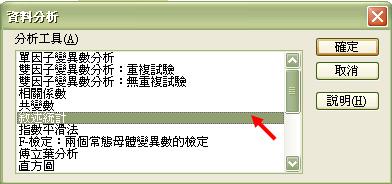
Excel 提供了一個快捷的方法去計算這些數字。假設我們想了解父親探究中樣本的年齡集中趨勢,我們可先打開工作頁,然後拉下「工具」表單,選擇「資料分析」:
然後選擇「敘述統計」
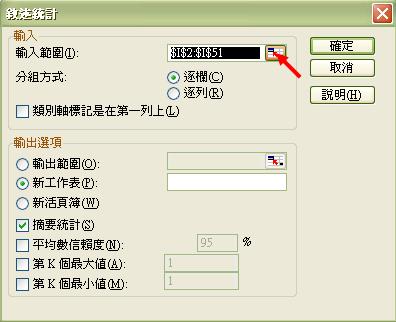
之後會彈出下左圖,我們需點擊箭咀指示的輸入範圍按鈕,再在彈出的右圖中按範圍圖示
|
|
|
 |
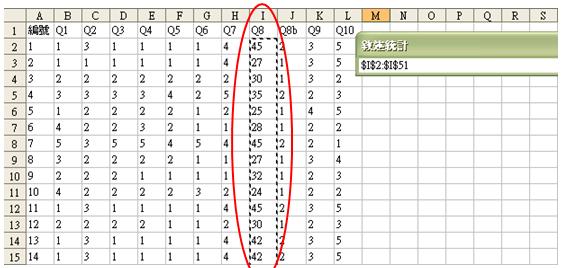
然後用滑鼠拖曳需要計算的數值範圍
(即 I2 至 I51)
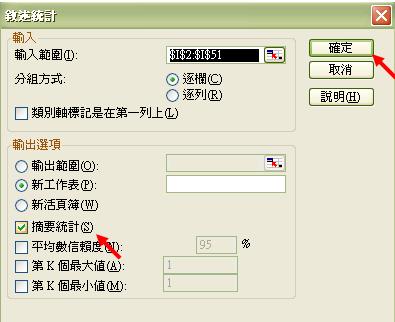
然後再按下左圖之箭咀位置,以確認選定數值。當我們返回描述統計的指令版面,便可選擇適用的輸出選項(如摘要統計),然後按「確定」進行統計:
 |
|
|
按「確定」出現的便是以下表列。以中學專題探究而言,暫且用不著使用表中所有數據,但最基本應知道平均數、中間值和眾數,及對變項變值的分佈形態有初步理解。
(c) 圖表分析
Excel 的圖表精靈提供多種圖表選項,專題報告中較常用的包括:
|
圖表類型 |
適用之測量尺度 |
功能 |
|
|
圓形圖 (pie chart) |
|
所有尺度 |
適用於顯示變項中不同變值之比例 |
|
直線圖 (bar chart) |
|
間斷 (類別和等級變項) |
- 概括和呈現不同組別的數據 |
|
群組直條圖 (grouped bar chart) |
|
繪製方法同上,不同的是X軸中每個類別都包括 兩個或以上的直條 |
|
|
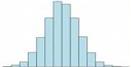
直方圖 (histogram) |
|
連續 (等距和等比變項) |
表達連續性資料的頻率分佈,以直方形的面積顯示個數的相對比例 |
|
折線圖 (line chart) |
|
連續 (等距和等比變項) |
用於趨勢分析,以線條的連續變化顯示變值之跨年升降 |
(d) 趨勢分析的示範
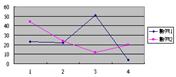
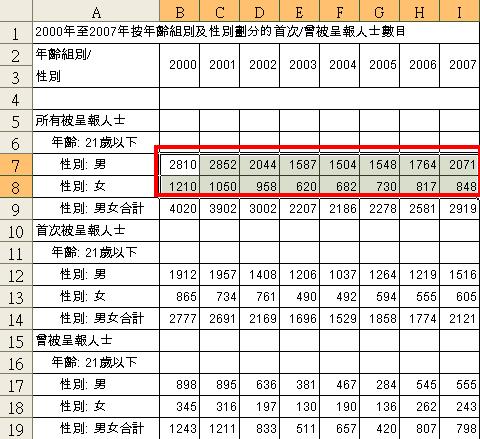
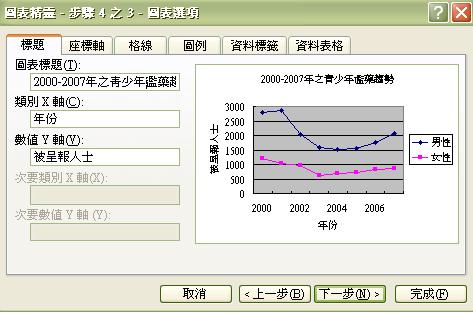
假設我們想探討2000-2007年間,21歲以下之年青人的吸毒趨勢,並在保安局禁毒處的網站下載相關資料的 Excel 檔案:
2000年至2007年按年齡組別及性別劃分的首次/曾被呈報人士數目(為方便示範,這個資料檔案經簡化及整理。按此到保安局網頁下載原本資料檔案。)
我們先打開工作頁,然後以滑鼠拖曳相關資料。
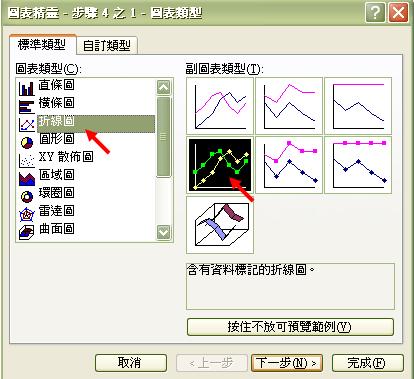
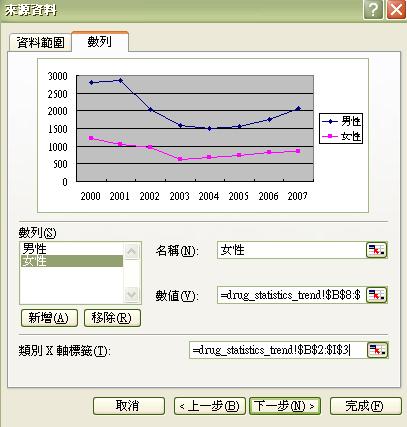
然後點擊圖表精靈,選項如下:
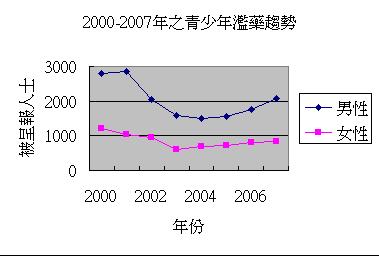
螢光幕便會出現圖表,顯示男性和女性的濫藥趨勢。我們只須在相關步驟中填上變項之名目,以及圖表標題和X、Y軸的資料,便能完成圖表。
|
|
|
|
進階課題 - 多變項分佈
(multivariate distribution) 和交互表列
Excel 提供多項分析工具,同學可在熟習以上技巧之後,進一步探索多於兩個變項之關係。詳見以下連結: